Fractales geométricos

En esta página tenemos una pequeña explicación de como surgen los módelos de fractales más típicos y más sencillos de dibujar con lápiz y regla:
 
Conjunto de Cantor
 

Se origina simplemente partiendo de un segmento de recta, lo dividimos en tres partes y eliminamos la parte central y así sucesivamente.

  
 
Triángulo de Sierpinski
 
Consiste en un triángulo en el que se aloja otro, uniendo los puntos medios de cada uno de sus lados. Esto se repite con todos y cada uno de los triángulos formados que tengan la misma orientación que el original, y así sucesivamente.
  
 
Curva de Koch
 
Se origina partiendo de un segmento, lo dividimos en tres partes y la parte central la sustituimos por dos segmentos (iguales al eliminado) formando un ángulo de 60º sobre la parte que se quita. Y así sucesivamente.
  
 
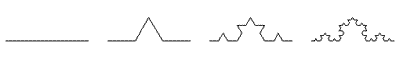Si en lugar de triángulos, simulamos cuadrados formaremos una curva llamada “punto de cruz”
  
 
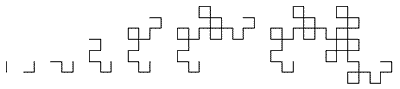
Curva del dragón
 
Se origina partiendo de un segmento que se repite, gira 90º y se añade a un extremo del anterior, la imagen formada se repite, gira 90º y se añade al extremo de la anterior, y así sucesivamente.
  
 
Curva de Peano
 
Partiendo de un segmento, lo dividimos en tres partes y en la parte central se dibuja a cada lado un cuadrado de longitud igual a la división realizada y así sucesivamente.